Write the value of sin^2 theta 1 (1 tan^2theta) · 1 – sin 2 θ = cos 2 θ √a 2 x 2 x = a tan θ 1 – tan 2 θ = sec 2 θ √x 2 − a 2 x = a sec θ sec 2 θ – 1 = tan 2 θSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more

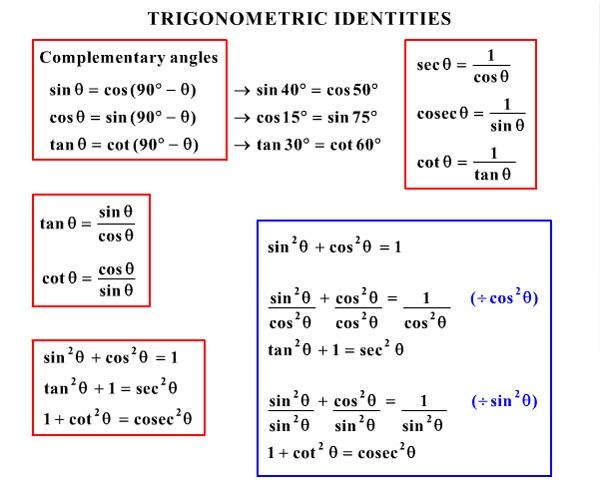
Trigonometric Identities
1-tan^2 theta/1+tan^2 theta formula
1-tan^2 theta/1+tan^2 theta formula-The Pythagorean Identity sin 2 θ cos 2 θ = 1 can be taken as sin 2 θ = 1 cos 2 θ and Equation (4) will become $\cos 2\theta = \cos^2 \theta (1 \cos^2 \theta)$ $\cos 2\theta = 2\cos^2 \thetaWrite the Value of `(Sin^2 Theta 1/(1Tan^2 Theta))` CBSE CBSE (English Medium) Class 10 Question Papers 6 Textbook Solutions Important Solutions 3111 Question Bank Solutions 334 Concept Notes & Videos & Videos 224 Time Tables 12
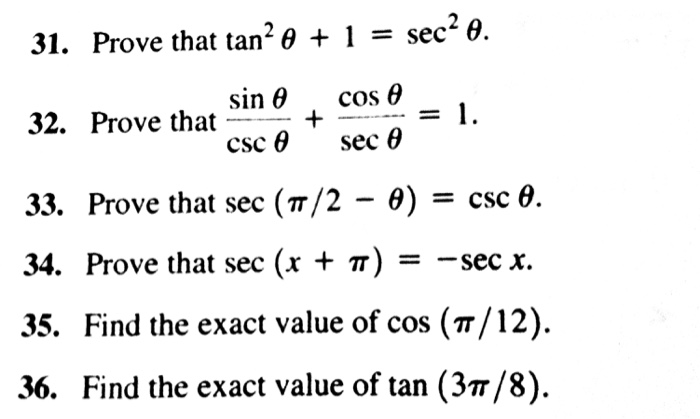


Solved 31 Prove That Tan 2 Theta 1 Sec 2 Theta 32 Chegg Com
0911 · Sine, tangent, cotangent and cosecant in mathematics an identity is an equation that is always true Meanwhile trigonometric identities are equations that involve trigonometric functions that are always true {2\tan \theta }}{{1{{{\tan }}^{2}}\theta }}$ Triple Angle IdentitiesAnswer to Verify the identity sec (theta)/1tan^2 (theta) = cos (theta) and we will look at an example of finding an equation representing a locus of points in a realworld settingTan theta = 1/2 tan theta = 1/2 Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW The most general solution of `tan theta =1 and cos theta = 1/sqrt 2 ` is0104 · $$\tan^{2}(\theta) 1 = \sec^{2}(\theta)$$ and $$\cot^{2}(\theta) 1 As 1st equation is not true for $\theta$ equals to Stack Exchange Network Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge,Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more
We need to prove `((1 tan^2 theta)cot theta)/(cosec^2 theta) = tan theta` Solving the LHS, we get `((1 tan^2 theta)cot theta)/(cosec^2 theta) = (sec^2 theta (cot theta))/(cosec^2 theta)` Using `sec theta = 1/cos theta, cot theta = cos theta/sin theta` `cosec theta = 1/sin thetaIf tan of theta is 1/2, what is the exact value of tan 2 theta Trigonometric Identity About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety HowB {eq}\tan^2\theta = 2\tan\theta1 {/eq} Trigonometric Equations A trigonometric equation consists of an equation where the variable appears as the argument of trigonometric functions


Solved 1 Tan Theta Tan Theta 1 Cos 2 Theta 1 Tan 2 Chegg Com


Solution 1 Amp Tan Amp 2 Amp 952 1 Amp Cot Amp 2 Amp 952 1 Tan A 1 Cot A 2
Prove the Following Trigonometric Identities (1 Tan^2 Theta)/(1 Cot^2 Theta) = ((1 Tan Theta)/(1 Cot Theta))^2 = Tan^2 Theta\tan^2(3\theta) = 1 \iff \sqrt{\tan^2(3\theta)} = \pm \sqrt 1 \iff \tan(3\theta) = \pm 1 Then \theta = \frac 13\tan^{1}(1)\tag{I} or \theta = \frac 13\tan^{1}(1)\tag{II} (I) \thetaPrave That If Tan θ 1 Tan θ = 2 , Then Show that Tan 2 θ 1 Tan 2 θ = 2 Maharashtra State Board SSC (English Medium) 10th Standard Board Exam Question Papers 238 Textbook Solutions Online Tests 39 Important Solutions 27 Question Bank Solutions 9421 Concept Notes &



Solved Prove The Following Identities Tan 2theta 2 Tan Chegg Com



1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube
1 tan 2 θ = 1 ( e i θ − e − i θ i ( e i θ e − i θ)) 2 = 1 − ( e i θ − e − i θ) 2 ( e i θ e − i θ) 2 = ( e i θ e − i θ) 2 − ( e i θ − e − i θ) 2 ( e i θ e − i θ) 2 = e 2 i θ 2 e − 2 i θ − e 2 i θ 2 − e − 2 i θ ( e i θ e − i θ) 2 = 4 ( e i θ e − i θ) 2 = ( 2 e i θ e − i θ) 2 = sec 2 θClick here👆to get an answer to your question ️ that \( \tan ^ { 3 } \theta \) \( 1 \tan ^ { 2 } \theta \) \( \cot ^ { 3 } \theta \) \( 1 \cot ^ { 2 } \theta · The expression is 1 tan2θ = 1 sin2θ cos2θ = cos2θ sin2θ cos2θ = 1 cos2θ = sec2θ Answer link Harish Chandra Rajpoot Jul 16, 18 1 tan2θ = sec2θ



Prove That Cot Theta 1 Tan Theta Cot Theta 2 Sec 2 Theta Maths Some Applications Of Trigonometry Meritnation Com



1 Tan Square Theta 2 3 Find Theta Brainly In
Something went wrong Wait a moment and try again Try again Please enable Javascript and refresh the page to continueIf `tan theta=1/2` and `tan phi =1/3`, then the value of `theta phi` is If `tan theta=1/2` and `tan phi =1/3`, then the value of `theta phi` is Watch later · According to my textbook, $\tan 2\theta = \frac{1}{119}$, but I get $\frac{10}{13}$ instead Stack Exchange Network Stack Exchange network consists of 176 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers
x-1=sec(squared)x.jpg)


10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com



5 1 5 2 Trigonometric Identities Ppt Download
Tan 2θ tan θ = 1 Using the formula tan 2A = 2 tan A/(1 – tan 2 A), (2 tan θ)/ (1 – tan 2 θ) tan θ = 1 2 tan 2 θ = 1 – tan 2 θ 3 tan 2 θ = 1 tan 2 θ = 1/3 tan θFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorClick here👆to get an answer to your question ️ Fill in the blankThe value of (1 tan^2 theta) (1 sintheta) (1 sintheta) =
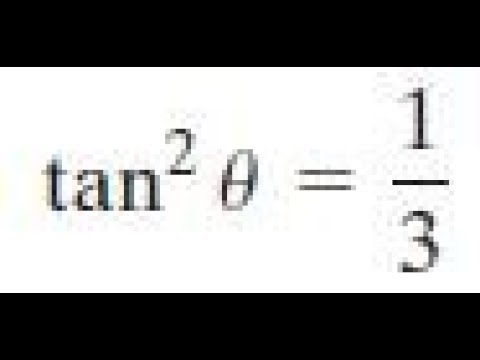


Tan 2 Theta 1 3 Solve For Interval 0 Less Theta Less 2pi Youtube



Simplify 1 Tan 2 Theta 1 Sin Theta 1 Cos Theta Brainly In
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreQuestion Solve 2 Tan Theta/3 Tan^2 Theta = 1 This problem has been solved!A point on (the right branch of) a hyperbola is given by (cosh θ, sinh θ) Projecting this onto y axis from the center (−1, 0) gives the following t = tanh 1 2 θ = sinh θ cosh θ 1 = cosh θ − 1 sinh θ {\displaystyle t=\tanh {\tfrac {1}{2}}\theta ={\frac {\sinh \theta }{\cosh \theta 1}}={\frac {\cosh \theta 1}{\sinh \theta }}}


How Do You Prove The Identity Sectheta Tantheta 2 1 Sintheta 1 Sintheta Socratic



Solved Establish The Identity 1 Tan 2 Theta 1 Tan 2 Chegg Com
1219 · Click here👆to get an answer to your question ️ A solution of the equation (1 tan theta) (1 tan theta) sec^2 theta 2^tan^2theta = 0 where theta lies in the interval (Learn about tangent 3 theta formula topic of Maths in details explained by subject experts on vedantucom Register free for online tutoring session to clear your doubtsGiven θ = 30° (1) To verify `tan 2 theta = (2 tan theta)/(1 tan^2 theta)` Now consider LHS of the expression to be verified in equation (2) Therefore LHS = `tan 2 theta` Now by substituting the value of θ from equation (1) in the above expression We get LHS = `tan 2 xx (30^@)` `= tan 60^@` `= sqrt3`



If Tan Theta Sec Theta 2 Then What Is Tan Theta Is Equal To Quora



The Number Of Roots Of The Equation Left 1 Tan Theta Right Left 1 Sin2 Theta Right 1 Tan Theta Theta In 0 2 Pi Is A 3 B 4 C 5 D None Of These Snapsolve
Cos θ = 1 – tan 2 (θ/2)/ 1 tan 2 (θ/2) 4/5 = 1 – tan 2 (θ/2)/ 1 tan 2 (θ/2) 4 4 tan 2 (θ/2) = 5 – 5 tan 2 (θ/2) 4 tan 2 (θ/2) 5 tan 2 (θ/2) = 5 – 4 9 tan 2 (θ/2) = 1 tan 2 (θ/2) = 1/9 tan θ/2Given that Tan ¢ 1/ Tan ¢ = 2 On squaring both sides we get, ( Tan ¢ 1/Tan ¢ )² = (2)² We know that, ( A B)² = ( A)² ( B)² 2 × A × B ( Tan² ¢ ) ( 1/Tan² ¢ ) 2 × Tan ¢ × 1/Tan ¢ = 4 ( Tan² ¢ ) ( 1/Tan² ¢ ) 2 = 4 ( Tan² ¢ ) ( 1/Tan² ¢ ) = 42Click here👆to get an answer to your question ️ If tan ^2theta = 2tan ^2ϕ 1, then cos 2theta sin ^2ϕ equals


Much From Little


Cochranmath Solving Trigonometric Equations
· $$3\tan^2\theta 1 =0$$ $$\tan^2\theta=\frac 13$$ $$\tan\theta=\pm\frac{\sqrt 3}3$$ For angles in the first quadrant, only $\frac\pi 6$ has a tangent of $\frac{\sqrt 3}3$, so that is our reference angle for our solutionsWe then find the corresponding angles in the other quadrants that have a tangent with the same absolute valueUsing this leads to \tan^2\alpha = \frac {\sin^2\alpha} {\cos^2\alpha}=\frac {1\cos^2\alpha} {\cos^2\alpha}=\frac {1} {\cos^2\alpha}1=\cos^2\theta\sin^2\theta A trigonometric identity is cos2x sin2x = 1 Using this leads to tan2α = cos2αsin2α = cos2α1−cos2α = cos2α1 −1 = cos2θ −sin2θ0121 · Using \(3\theta = 2\theta \theta \), the addition Equation for sine, and the doubleangle Equations \ref{eqndoublesin} and \ref{eqndoublecosalt2}, we get


Prove That Math Tan 2 Theta 1 Sec 2 Theta Math Quora



If Theta 30 Verify That Tan 2theta 2 Tan Theta 1 Tan Square Theta Maths Introduction To Trigonometry Meritnation Com
By addition formula of tan, Here, Thus, Thus proved Learn more Prove that tan2 theta/tan 2 theta1 cosec 2 theta/sec 2 theta cosec 2 theta =1/sin 2 theta cos2 theta brainlyin/question/ If cot b = 12/5 Prove that tan2 b sin2 b = sin 4 b x sec2 b brainlyin/question/See the answer Show transcribed image text Expert Answer Previous question Next question Transcribed Image Text from this Question Solve 2 tan theta/3 tan^2 theta = 1 Get more help from Chegg · In engineering fields such as mechanical engineering, electronics, and mechatronics, the analytical use of trigonometry is important So, with basics of the tan theta formula we can easily solve and simplify higherorder problems such as 1 tan theta, tan 3 theta, tan 3 theta, tan 3 theta 1 tan 2 theta, tan3x formula and so on



Prove The Following Identitie See How To Solve It At Qanda
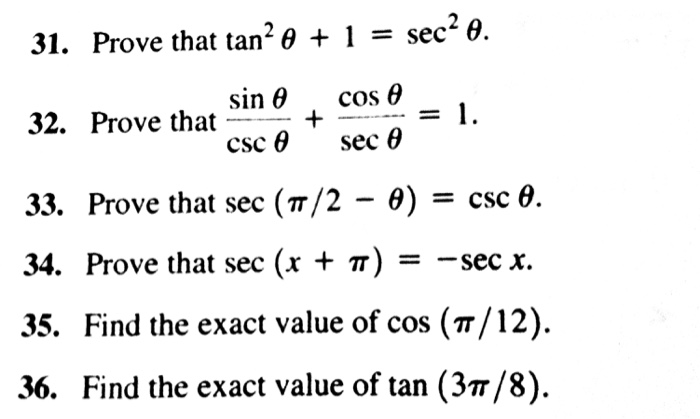


Solved 31 Prove That Tan 2 Theta 1 Sec 2 Theta 32 Chegg Com



Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions



1 1 Tan 2 Theta 1 1 Cot 2 Theta 1 Sin 2 Theta Sin 4 Theta Brainly In


Solved 1 Tan2 Theta Sec2 Theta Verify That The Equati Chegg Com


What Is The Formula Of Tan2x Quora
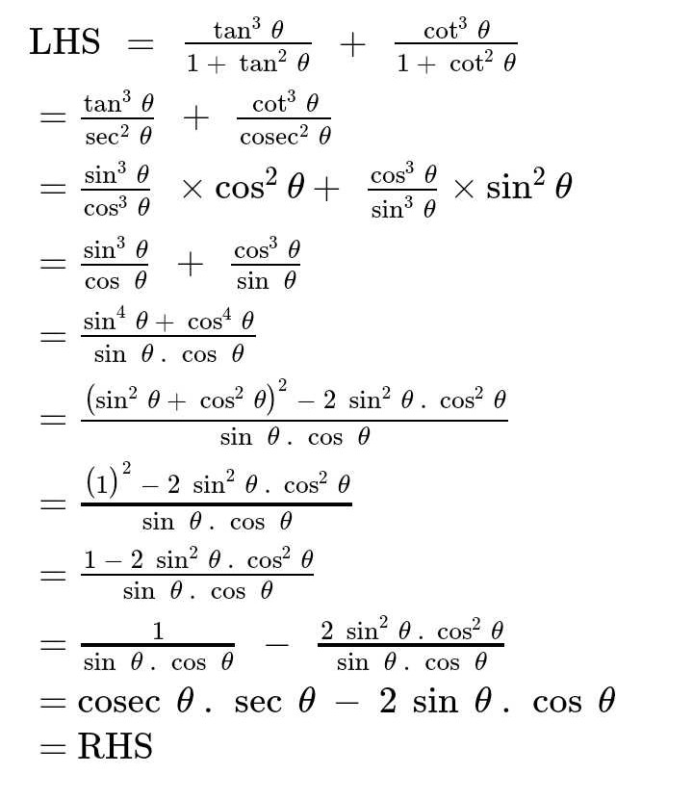


Prove If Tan 3 Theta 1 Tan 2 Theta Cot 3 Theta 1 Cot 2 Theta Sec Theta Cosec Theta 2 Sin Theta Cos Theta Edurev Class 10 Question



Solved Prove The Given Identity Cos 2 Theta 1 Tan2 Th Chegg Com


How Do You Prove 1 Sin 2theta 1 Cot 2theta Cot 2theta Socratic



Worksheet On Finding The Unknown Angle Using Trigonometric Identities
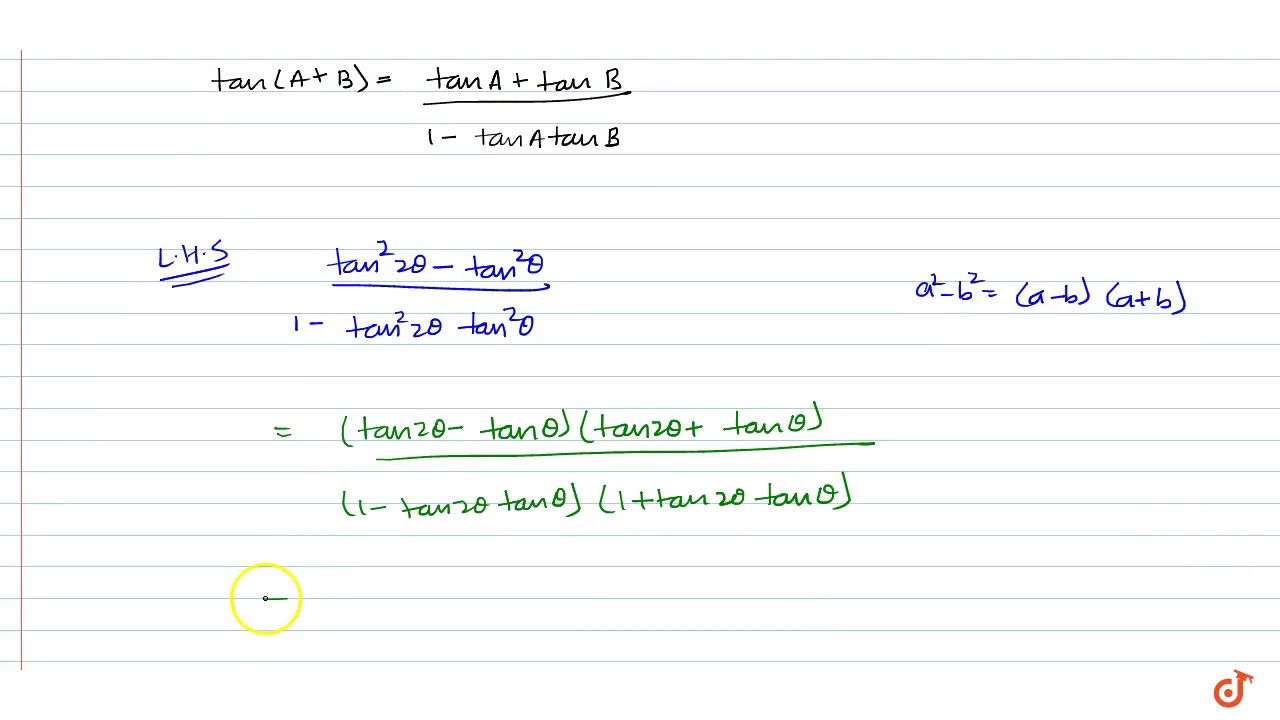


Prove That Tan 2 2theta Tan 2 Theta 1 Tan 2 2theta Tan 2 Theta Tan 3theta Tan Theta Youtube


Prove That Tan 8 1 Cot 8 Cot 8 1 Tan 8 1 Tan8 Cot 8 Studyrankersonline



Tan 2 Theta Cos 2 Theta 1 Cos 2 Theta Brainly In



Solve The Equation Tantheta Tan 2theta Tan 3theta 0



5 1 Fundamental Trig Identities Sin 1cos 1tan 1 Csc Sec Cot Csc 1sec 1cot 1 Sin Cos Ppt Download



30 The Number Of Roots Of The Equation 1 Tan Theta 1 Sin 2 Theta 1 Tan Theta For Theta In 0 2 Pi Is 2 C 5 0 4 D None Of These



Trigonometrical Ratios Or Functions A Plus Topper



Sin 2 Theta Is Equal To 2 Tan Theta Upon 1 Tan Square Theta And Theta 30 Degree Brainly In



Double Angle Formula And Half Angle Formula Video Lessons Examples And Solutions



If 1 Sin 3 Sin Cos Then Show That Tan 1 Or 1 2 Mathematics Topperlearning Com 328h6ymm


How I Remember Trig Identities Part 2 Beyond Solutions


5 1 Fundamental Trig Identities Sin 1cos 1tan 1 Csc Sec Cot Csc 1sec 1cot 1 Sin Cos Ppt Download



How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic



Art Of Problem Solving
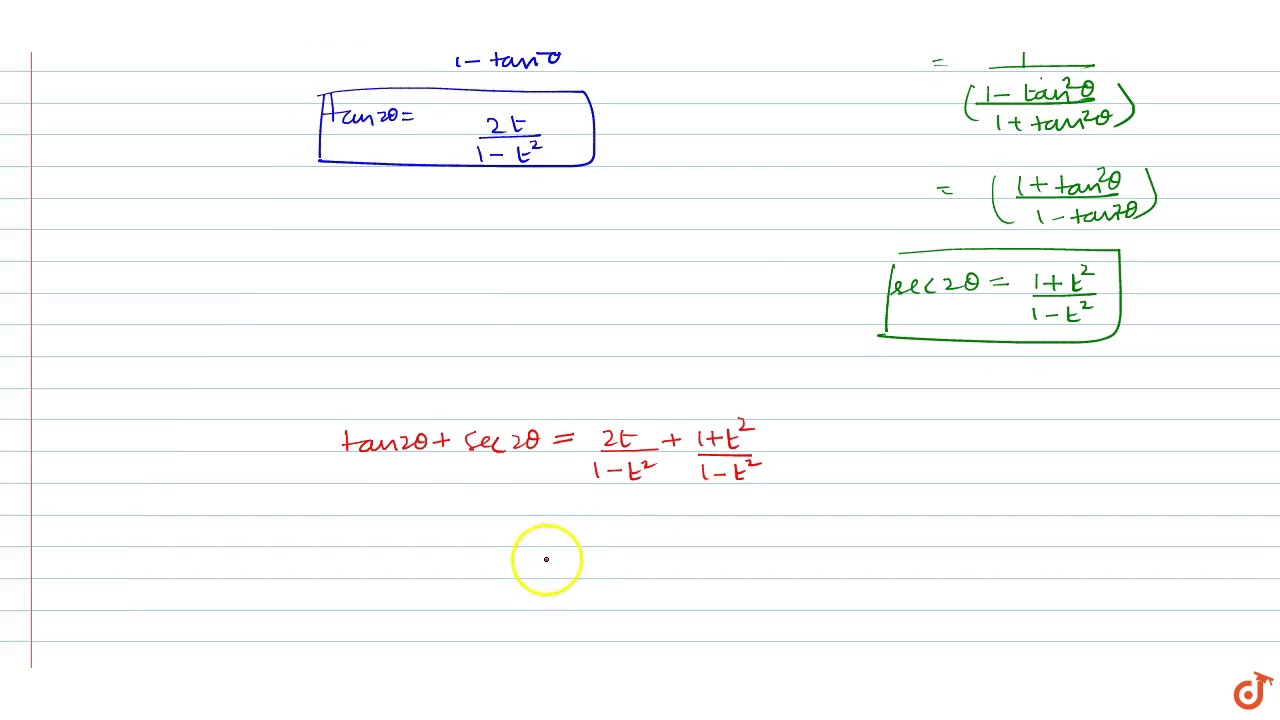


If Tan Theta T Then Tan 2 Theta Sec 2 Theta Youtube



Prove That 1 Tan Theta Tan 2theta Sec 2theta Youtube



Prove That 1 Tan 28 1 Cot 28 1 Tan8 1 Cot8 2 Tan 28
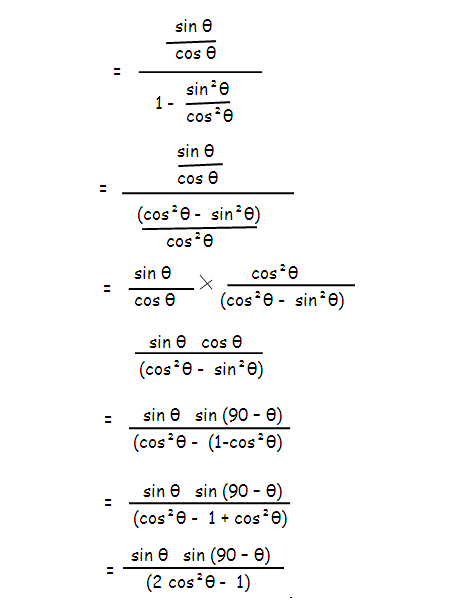


Trigonometric Identities Examples


18 Find The Cartesian Equation Of The Curve From The Parametric Equations X Tan 2 Theta And Y Sec Theta Where Pi 2 Theta Pi 2 Then Sketch It Width Indication Of


Derivatives Of Trigonometric Functions



Cos 2 Theta 1 Tan Theta Sin 3 Theta Sin Theta Cos Theta 1 Sin Theta Cos Theta Brainly In



त र क णम त य सर वसम क ओ क स च व क प ड य Trigonometric Functions Math Methods Math Formulas



Tangent Half Angle Formula Wikipedia
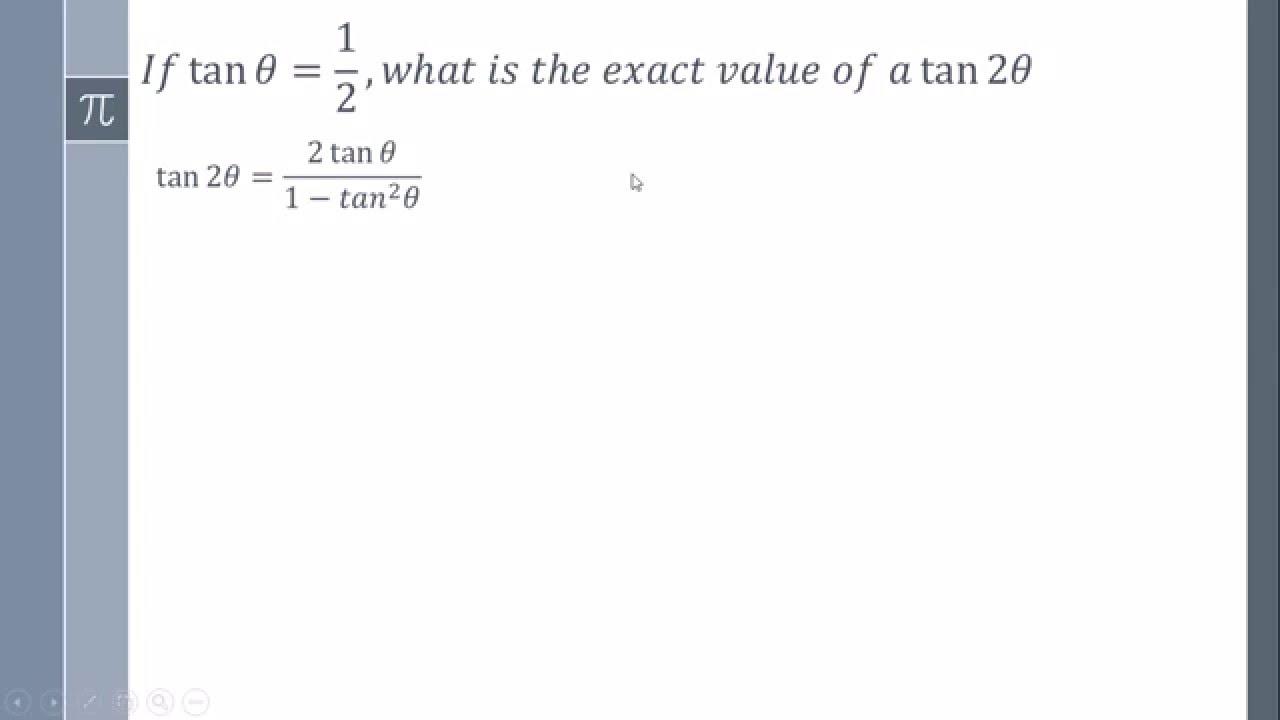


If Tan Of Theta Is 1 2 What Is The Exact Value Of Tan 2 Theta Youtube


Solution Prove Sin 2theta 2tan Theta 1 Tan 2 Theta



Proof Tan 2 1 Sec 2 Youtube


How To Solve The Equation 2 Tan Theta Cot Theta 1 Quora


Prove That Math Tan 2 Theta 1 Sec 2 Theta Math Quora
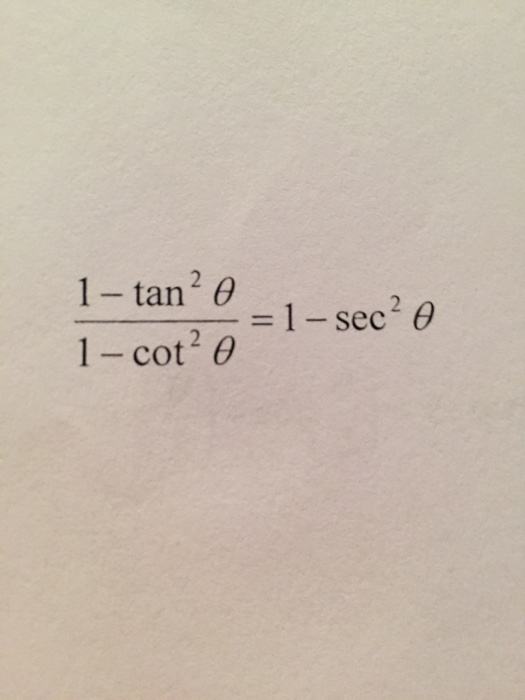


Solved 1 Tan 2 Theta 1 Cot 2theta 1 Sec 2theta Ve Chegg Com



Prove That Tan 2 Theta 1 Tan 2 Theta Cot 2 Theta 1


Trigonometry Trigonometric Laws And Identities



Using Trigonometric Identities Video Khan Academy



Tan 4 Theta 4 Tan Theta 1 Tan 2 Theta 1 6 Tan 2 Theta Tan 4 Theta Maths Trigonometric Functions Meritnation Com



Summary Of Trigonometric Identities



Trouble Applying The Tan Double Angle Formula For 5 Tan 2 Theta 4 Cot Theta Mathematics Stack Exchange
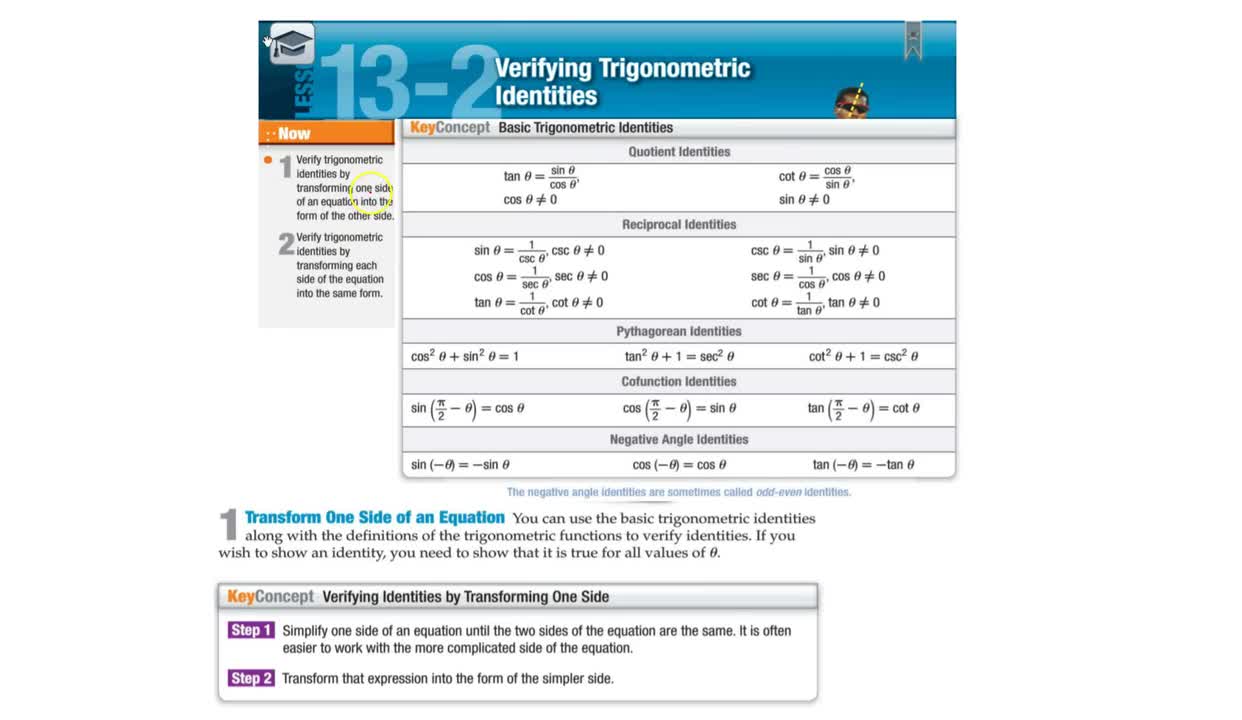


Honors Algebra 2 Trig Notes Chapter 13 Section 2 Bishop Amat Memorial High School



1 Tan 2theta 1 Cot 2theta 1 Tan Theta 1 Cot Theta 2 Tan 2 Theta Brainly In



Solved Verify Prove The Following Trigonometric Identit Chegg Com



Prove That Cot 8 Tan 8 2 Cos 2 8 1 Sin 8 Cos 8
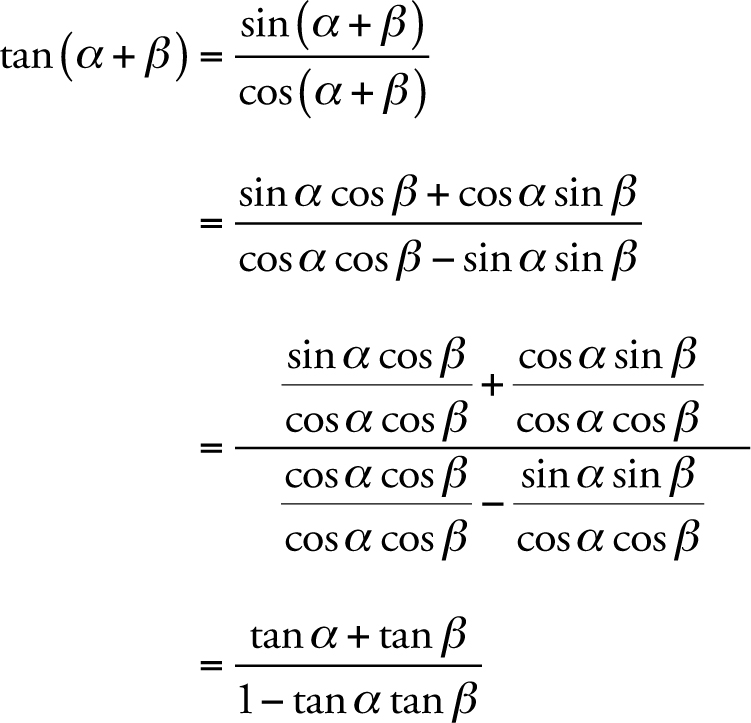


Tangent Identities


How Do You Verify Tan 28 Sin 28 Tan 28sin 28 Socratic
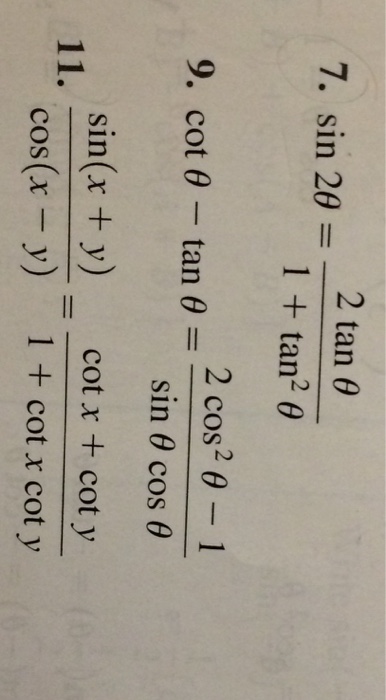


Solved Sin 2 Theta 2 Tan Theta 1 Tan 2 Theta Cot Thet Chegg Com



Tangent Half Angle Formula Wikipedia



Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf



Prove That 1 1 Tan 2 Theta 1 1 Cot 2 Theta 1


If Tan Theta Cot Theta 2 Then What Is The Value Of Tan Squared Theta Cot Squared Theta Equal To Quora


Prove That 1 Tan 2 8 1 Cot 2 8 1 Tan 8 Cot 8 2 Tan 2 8 Sarthaks Econnect Largest Online Education Community



What Is The Formula For Tan 2 Theta



What Is The Value Of Sin 2theta 1 1 Tan 2theta



If Theta 60 Then 1 Tan 2 Theta 2tan Theta Is Equal To


If Tan 8 1 2 And Tan ϕ 1 3 Then The Value Of 8 ϕ Is Studyrankersonline



7 6 Double Angle Half Angle Formulas Flashcards Quizlet



Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo



How Does The Trigonometric Identity 1 Cot 2 Theta Csc 2 Theta Derive From The Identity Sin 2 Theta Cos 2 Theta 1 Mathematics Stack Exchange



Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo



Solved Use The Trigonometric Identities To Simplify The E Chegg Com



Trigonometric Identities



How Do You Prove Tan 2x Secx 1 1 Secx Socratic
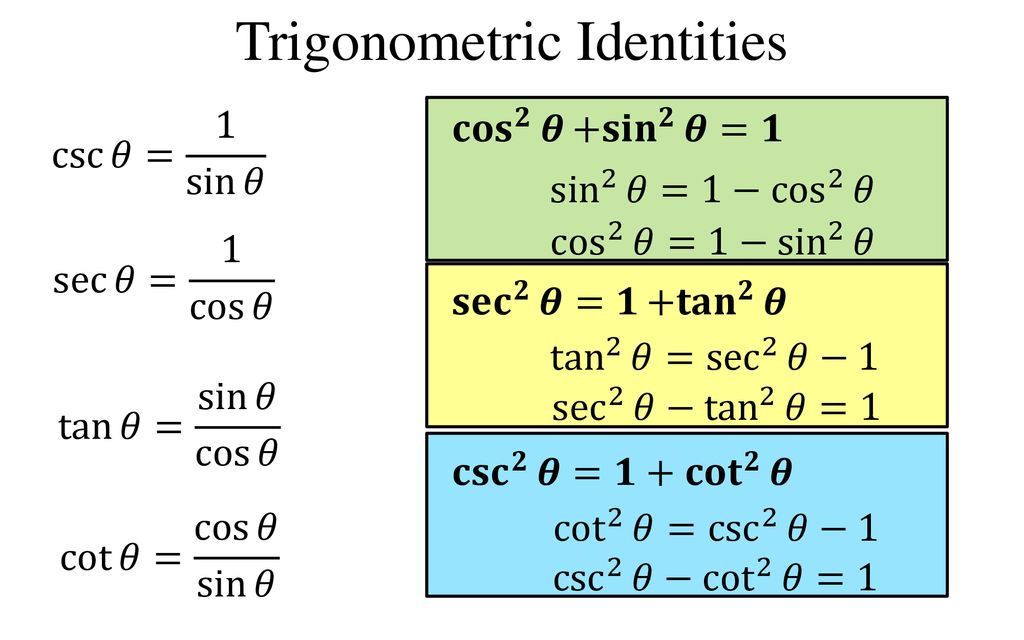


Trigonometric Identities And Equations Ppt Download


If Tan 2theta 1 2tan 2a Then Prove That 2sin 2theta 1 Sin 2a Mathematics Topperlearning Com 47



3 Simplifying Trig Expression 1 Tan 2x Youtube



Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf



Tan Theta 1 Tan 2 Theta 2 Cot Theta 1 Cot 2 Theta 2 Sin Theta Cos Theta Brainly In



Solve The Equation 1 Tan Theta 1 Sin 2theta 1 Tan Theta



Proofs Of Trigonometric Identities Wikipedia



Sec 2 Theta 1 Tan 2 Theta Youtube



Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf



Tangent Half Angle Formula Wikipedia


Solving Trigonometric Equations With Identities Precalculus Ii



Prove That Tan 3 Theta 1 Tan 2theta Cot 3 Theta 1 Cot 2 Theta



Solve The Following Equation Tan 2theta Sec 2theta 3 2 Sqrt 2



0 件のコメント:
コメントを投稿